In this column, I would like to write about how to move particles. I also would like to write about how to calculate the acceleration of a particle because a particle’s displacement is expressed by “Distance = Velocity × Time”*1 and the acceleration is necessary to update the particle’s velocity.
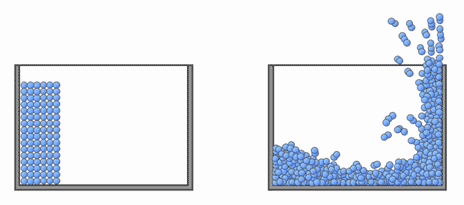
4.1 How to move particles
We move particles as follows:
[0] Set the initial coordinates*2 and velocities*3 of all the particles.
[1] Calculate the accelerations of particles by the Navier‒Stokes equations.
[2] Update the velocities of particles by the calculated accelerations
[3] Move the particles by the updated velocities
[4] Return to the procedure [1], and continue the procedures [1] to [3]*4.
That’s all. Very simple, isn’t it?
4.2 How to calculate the accelerations of particle
The accelerations of particles are calculated by the Navier‒Stokes equations, which is the equation of motion for fluid. First, I would like to explain the equation of motion for a material particle, instead of fluid particle because the equation of motion for a material point is simpler than the Navier‒Stokes equations. The equation of motion for a material particle is expressed as follows:
$$ \boldsymbol{m} \boldsymbol{a}=\boldsymbol{F} $$where \(\boldsymbol{m}\) is the mass of the material particle, \(\boldsymbol{a}\) is the acceleration of the material particle and \(\boldsymbol{F}\) is the force acting on the material particle. By dividing the both sides of Eq.(1) by \(\boldsymbol{m}\), we obtain the following equation:
$$ \boldsymbol{a}=\frac{\boldsymbol{F}}{\boldsymbol{m}} $$From the above equation, we can find that the acceleration of a material particle is in proportion to the force, and is in inverse proportion to the mass. If we calculate the right hand side of Eq.(2), which is the force divided by the mass, we can obtain the acceleration of a material point. In the same manner, the acceleration of a fluid particle is obtained by dividing the force acting on a fluid particle by the mass of the fluid particle as follows:
$$ \boldsymbol{a}=-\frac{1}{\rho} \nabla P+\nu \nabla^{2} \boldsymbol{u}+\boldsymbol{g} $$The above equations are the Navier‒Stokes equations. Although various symbols are used in Eq.(3), these equations are not so difficult. The right hand side of Eq.(3) is composed of three terms of acceleration because three forces*5 act on a fluid particle. By calculating the right hand side of Eq.(3), we can obtain \(\boldsymbol{a}\), which is the acceleration of a fluid particle. For the meaning of each term on the right hand side of Eq.(3), see the footnote*6. For the concrete calculation of these terms, see the reference book1).
Reference:
1. 越塚誠一, 柴田和也, 室谷浩平, 粒子法入門, 丸善出版, 2014年6月25日, ISBN-13: 978-4621088340
Footnotes:
*1: In the sentence, the time means the time increment \(\Delta\boldsymbol{t}\), which is a small time period such as 0.001 s.
*2: In general, particles are arranged at regular intervals at the initial state. The interval is called the initial distance between particles, and is the parameter which expresses the particle size and the spatial resolution.
*3: The initial velocity is set according to the problem we need to solve. For example, if the fluid is stationary at the initial state, the velocities of all the fluid particles are set to 0.0m/s.
*4: In a case where an implicit pressure calculation is applied, additional procedures are necessary.
*5: In a case where the surface tension or other external forces work, the acceleration is composed of more than 3 terms.
*6: The first term \(-\frac{1}{\rho} \nabla P\) on the right hand side of Eq.(3) is the term about acceleration due to pressure. From the term, we can find that the acceleration due to pressure is in proportion to the pressure gradient \( P\) and is in inverse proportion to the fluid density \(\rho\). The minus sign before \(\nabla P\) is necessary because the force due to the pressure gradient works in the direction whose pressure is the lowest. The second term of \(\nu \nabla^{2} \boldsymbol{u}\) is the viscosity term, which is the acceleration vector due to viscosity. The viscosity term diffuses the momentum of fluid. The coefficient \(\nu\) is the kinematic viscosity coefficient. The third term \(\boldsymbol{g}\) is the acceleration vector due to the gravity.
TOC
Introduction to the particle method
- What is a particle method?
- In what ways is the particle method different from other methods?
- Mass and volume of particles
- How to move particles and how to calculate accelarations of particles
- How to shorten the simulation time
About The Author

Kazuya Shibata, Ph.D.
Assistant Professor at Department of System Innovation, Graduate School of Engineering, The University of Tokyo.
