まずは,SPH法における空間離散化方法から説明します.SPH法では,連続関数をカーネル近似で近似してから,その近似式を使って粒子を使った空間の離散化へと発展します.3次元(あるいは2次元) の領域\( \Omega\)上で定義される場のスカラー関数\( \phi\)は,領域内の任意の点\( \boldsymbol{x}\)にて,ディラックのデルタ関数\( \delta\)を使った体積積分として表示します.
$$ \phi(\boldsymbol{x})=\int_{\Omega} \phi(\boldsymbol{\xi}) \delta(\boldsymbol{\xi}-\boldsymbol{x}) \mathrm{d} \boldsymbol{\xi} $$ここで,体積積分を意味する記号\(\int_{\Omega}(\cdot) \mathrm{d} \boldsymbol{\xi}\)における被積分関数は,変数\(\boldsymbol{\xi}\)関数とし,体積積分することを意味しています.またディラックのデルタ関数は
$$ \delta(\boldsymbol{x})=\left\{\begin{array}{ll} \infty, & \boldsymbol{x}=\mathbf{0} \\ 0, & \boldsymbol{x} \neq \mathbf{0} \end{array}\right. $$を満たし,\(\phi(\boldsymbol{x})=1\)の定数関数を考えれば,次の特性をもちます.
$$ \int_{\Omega} \delta(\boldsymbol{\xi}) \mathrm{d} \boldsymbol{\xi}=1 $$\( \delta\)は原点で関数値が\( \infty\)かゼロとなる,かなり尖った関数*1とみなせます.SPH法では,この尖った関数の代わりに,
*1 形だけでなく,数学の関数としても超関数と言われるちょっと変わった関数である.
\(\phi^{\mathrm{SPH}}(\boldsymbol{x})\)を\(\phi(\boldsymbol{x})\)のカーネル近似,そしてこの滑らかな関数\(w_{h}^{\mathrm{SPH}}\)をカーネル関数と呼びます.\(h\)は平滑化の対象を決める領域(半径) を示すものとし,SPH法では次の条件を満たす関数からカーネル関数を選択します.
$$ \text { (コンパクトサポート条件) } \quad w_{h}^{\mathrm{SPH}}(|\boldsymbol{\xi}-\boldsymbol{x}|)=0, \quad|\boldsymbol{\xi}-\boldsymbol{x}| \geq h $$ $$ \text { (ユニティ条件) }\quad \int_{\Omega} w_{h}^{\mathrm{SPH}}(|\boldsymbol{\xi}-\boldsymbol{x}|) d \boldsymbol{\xi}=1 $$今考えている近似式(5)は,デルタ関数を使った積分表示の式(4)の近似をしていることになり,コンパクトサポート条件(6),ユニティ条件(7)は,それぞれディラックのデルタ関数の性質(2)と(3)に対応しています.元の積分表示ではダミー変数\(\boldsymbol{\xi}\)から観測点\( \boldsymbol{x}\)の関数値のみを抽出するため,デルタ関数\(\delta(\boldsymbol{\xi}-\boldsymbol{x}) \)を作用させていました.これに対し,SPH法におけるカーネル近似は,「観測点近傍の点も平滑化に取り入れるために,観測点\( \boldsymbol{x}\)からの相対距離\( |\boldsymbol{\xi}-\boldsymbol{x}|\)が一定の半径\(h\)内にいる近傍\(\boldsymbol{\xi}\)での値を使った重み付き平均」をしていることになります.コンパクトサポート条件は,「重み付き平均の対象を一定の半径\(h\)内にいる近傍に限定する」ことを表わしています.また,その平滑化のための重みがカーネル関数\(w_{h}^{\mathrm{SPH}}(|\boldsymbol{\xi}-\boldsymbol{x}|) \)であり,相対距離に応じた重みを与えます. そして,ユニティ条件は,影響半径\(h\)をゼロに収束させたときに,カーネル関数がデルタ関数に収束させるための必要条件です.つまり,影響半径を小さくしていくとユニティ条件を満足させるため,各点の重みは大きくなり,究極に観測点まで収束させれば無限大の重み,すなわちディラックのデルタ関数になるべきであることを意味しています.
この滑らかな関数を使った積分形式のカーネル近似がSPH法の基礎であり,SPH法(Smoothed Particle Hydrodynamics) の名前の由来にもなっています.デルタ関数をカーネル関数に変更した 式が近似として十分に成立しているのか,テイラー展開を使って考えてみます.コンパクトサポート条件より,被積分関数の中に登場するダミー変数\(\boldsymbol{\xi}\)は観測点\( \boldsymbol{x}\)近傍の点として考えられます.この観測点近傍での関数値\(\phi(\boldsymbol{\xi})=\phi(\boldsymbol{x}+\Delta \xi)\)を固定した観測点*2周りでテイラー展開すれば
$$ \phi(\boldsymbol{\xi})=\phi(\boldsymbol{x})+\frac{\partial \phi}{\partial \boldsymbol{\xi}}(\boldsymbol{x}) \cdot \Delta \boldsymbol{\xi}+\frac{1}{2} \Delta \boldsymbol{\xi} \cdot \frac{\partial^{2} \phi}{\partial \boldsymbol{\xi}^{2}}(\boldsymbol{x}) \Delta \boldsymbol{\xi}+\mathcal{O}\left(\Delta \boldsymbol{\xi}^{3}\right) $$ $$ =\phi(\boldsymbol{x})+(\boldsymbol{\xi}-\boldsymbol{x}) \cdot \frac{\partial \phi}{\partial \boldsymbol{\xi}}(\boldsymbol{x})+\mathcal{O}\left(\Delta \boldsymbol{\xi}^{2}\right) $$*2 近傍のすべての点で同じ観測点を使ってテイラー展開する.
となります.ここで\(\Delta \boldsymbol{\xi}=\boldsymbol{\xi}-\boldsymbol{x}\)であり,以降は\(\Delta \boldsymbol{\xi}\)の1次の項までで近似することにします.
このテイラー展開式(9) を式(5) に代入すると
$$ \begin{equation} \begin{aligned} \phi^{\mathrm{SPH}}(\boldsymbol{x}) &=\int_{\Omega} \phi(\boldsymbol{\xi}) w_{h}^{\mathrm{SPH}}(|\boldsymbol{\xi}-\boldsymbol{x}|) \mathrm{d} \boldsymbol{\xi} \\ &=\int_{\Omega}\left\{\phi(\boldsymbol{x})+(\boldsymbol{\xi}-\boldsymbol{x}) \cdot \frac{\partial \phi}{\partial \boldsymbol{\xi}}(\boldsymbol{x})\right\} w_{h}^{\mathrm{SPH}}(|\boldsymbol{\xi}-\boldsymbol{x}|) \mathrm{d} \boldsymbol{\xi}+R \end{aligned} \end{equation} $$ $$ =\phi(\boldsymbol{x}) \int_{\Omega} w_{h}^{\mathrm{SPH}}(|\boldsymbol{\xi}-\boldsymbol{x}|) \mathrm{d} \boldsymbol{\xi}+\frac{\partial \phi}{\partial \boldsymbol{\xi}}(\boldsymbol{x}) \cdot \int_{\Omega}(\boldsymbol{\xi}-\boldsymbol{x}) w_{h}^{\mathrm{SPH}}(|\boldsymbol{\xi}-\boldsymbol{x}|) \mathrm{d} \boldsymbol{\xi}+R $$ $$ =\phi(\boldsymbol{x}) \int_{\Omega} w_{h}^{\mathrm{SPH}}\left(\left|\boldsymbol{\xi}^{\prime}\right|\right) \mathrm{d} \boldsymbol{\xi}^{\prime}+\frac{\partial \phi}{\partial \boldsymbol{\xi}}(\boldsymbol{x}) \cdot \int_{\Omega} \boldsymbol{\xi}^{\prime} w_{h}^{\mathrm{SPH}}\left(\left|\boldsymbol{\xi}^{\prime}\right|\right) \mathrm{d} \boldsymbol{\xi}^{\prime}+R $$となります.\(R\)は式(9)の\(\mathcal{O}\left(\Delta \boldsymbol{\xi}^{2}\right)\)に関連する誤差です.式(10)から式(11)への式変形では,被積分関数はダミー変数\(\boldsymbol{\xi}\)の関数として考えるので,\(\phi(\boldsymbol{x})\)と\(\frac{\partial \phi}{\partial \boldsymbol{\xi}}(\boldsymbol{x})\)は固定した観測点\(\boldsymbol{x}\)での値となり,積分の外に出せます.また,式(11)と式(12)は,\(\boldsymbol{\xi}-\boldsymbol{x}\)は観測点\(\boldsymbol{x}\)を中心とした相対位置を意味しており,これを\(\boldsymbol{\xi}^{\prime}\)と表わしています.結局,式(11)に示すカーネル近似\(\phi^{\mathrm{SPH}}(\boldsymbol{x})\)が関数\(\phi(\boldsymbol{x})\)の近似として成立するためには,次の2つの条件を満足させればよいことになります.
$$ \int_{\Omega} w_{h}^{\mathrm{SPH}}\left(\left|\boldsymbol{\xi}^{\prime}\right|\right) \mathrm{d} \boldsymbol{\xi}^{\prime}=1 $$ $$ \int_{\Omega} \boldsymbol{\xi}^{\prime} w_{h}^{\mathrm{SPH}}\left(\left|\boldsymbol{\xi}^{\prime}\right|\right) \mathrm{d} \boldsymbol{\xi}^{\prime}=0 $$初めの式は,観測したい点\(\boldsymbol{x}\)周辺で定義するカーネル関数は領域で積分すると“1”となるべきであることを示しており,既出のユニティ条件と呼ばれるカーネル近似のための条件です.そして,2つ目の条件は,カーネル関数が偶関数(原点対称な変数で関数値が等しい関数)
$$ w_{h}^{\mathrm{SPH}}\left(\left|\boldsymbol{\xi}^{\prime}\right|\right)=w_{h}^{\mathrm{SPH}}\left(\left|-\boldsymbol{\xi}^{\prime}\right|\right) $$であれば満足しますが,これはカーネル関数を距離\(r=|\boldsymbol{\xi}-\boldsymbol{x}|\)の関数として設定したことから,自動的に満足する特性です. このカーネル関数の特性より,\(\boldsymbol{\xi}^{\prime} w_{h}^{\mathrm{SPH}}\left(\left|\boldsymbol{\xi}^{\prime}\right|\right)\)は奇関数となり先の条件式(14)を満足することがわかります.そして最後に,数値シミュレーションをするときに少しでも計算負荷を小さくしたい(領域積分の範囲を少しでも狭く設定したい)との要望から(コンパクトサポート条件) を加えています.カーネル関数に与えれる必要条件(と要望) が揃いました.以上,すべての条件を下記にまとめて示します.
(1. ユニティ条件)
(2.偶関特性(= 距離r の関数とする)
(3.コンパクトサポート条件)
(4.非負性条件)
(5.デルタ関数への収束条件)
(6.単調減少条件)
(7.微分連続性)
2階微分までが連続な関数を選択することが多い.
以上の7つの条件を満足するカーネル関数\(w_{h}^{\mathrm{SPH}}\)として,できるだけ単純な関数を選択する方針から,SPH法の数値シミュレーションでは3次スプライン関数と5次スプライン関数と呼ばれる区分多項式が用いられることが多いです(図1参照).
$$ w_{h}^{\mathrm{SPHc}}(r)=\alpha_{d}^{\mathrm{c}}\left\{\begin{array}{ll} 1-6(r / h)^{2}+6(r / h)^{3}, & 0 \leq r / h<1 / 2, \\ 2(1-r / h)^{3}, & 1 / 2 \leq r / h<1, \\ 0, & r / h \geq 1, \end{array}\right. $$ $$ w_{h}^{\mathrm{SPHq}}(r)=\alpha_{d}^{\mathrm{q}}\left\{\begin{array}{ll} (1-r / h)^{5}-6(2 / 3-r / h)^{5}+15(1 / 3-r / h)^{5}, & 0 \leq r / h<1 / 3, \\ (1-r / h)^{5}-6(2 / 3-r / h)^{5}, & 1 / 3 \leq r / h<2 / 3, \\ (1-r / h)^{5}, & 2 / 3 \leq r / h<1, \\ 0, & r / h \geq 1 . \end{array}\right. $$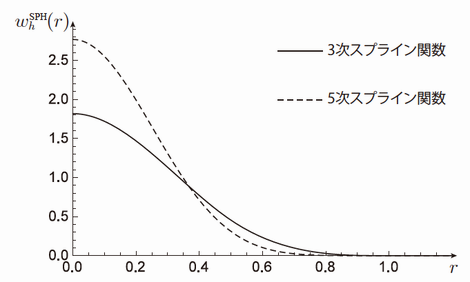
ここで,\(\alpha_{d}^{c}\)と\(\alpha_{d}^{\mathrm{q}}\)はユニティ条件(7)を満たすための定数で,\(\alpha_{d}^{c}=10 / 7 \pi h^{2} \)(2次元), \(1 / \pi h^{3} \) (3次元),\(\alpha_{d}^{\mathrm{q}}=15309 / 478 \pi h^{2}\)(2次元),\(2187 / 40 \pi h^{3} \) (3次元) として影響半径を設定すれば,事前に決められます.上記に示したスプライン関数は区分多項式になっているので場合分けが必要のため,場合分けが不要なWendland関数[8]も使われることもあります.
参考文献:
[8] H. Wendland: Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree, Advances in Computational Mathematics volume 4, 389–396, 1995.


