第2回 粒子法は、他の方法とどう違うか | 粒子法入門

前回のコラムでは、粒子法を使えば様々な難しい問題を容易にシミュレーションできることを紹介しました。粒子法はなぜそのようなことをできるのでしょう。今回のコラムでは、粒子法を他の計算手法と比較することでその理由を説明したいと思います。

1. 差分法

流体シミュレーションの伝統的な計算手法として、差分法があります。差分法を使ってパイプの中の水の流れ（図１）を計算する際の様子を図２に示します。計算領域を網目のような格子（計算格子）に分割して考え、格子のある位置（四辺形の中心や、１辺の中央など）に計算点（計算上の観測点のようなもの）を置きます。それらの計算点に、変数（圧力、速度、流体密度、温度などの値）の情報を持たせ、時間が経過するとともに変数の値を更新していきます。差分法では、格子を移動させたり変形したりすることは基本的には行いません注1ので、計算点も移動しません。つまり空間に固定された同じ位置で流れを観測することになります。温度の時間変化を求める場合で考えると、差分法ではある場所に温度計を固定して温度を測り続けることになります。場所を固定していますので、毎時刻においてその位置を通過する別の流体の温度を測定（計算）していることになります。

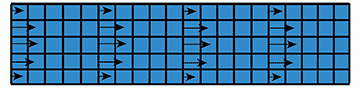
（矢印は流速を表しています。本当は全ての格子の各辺に垂直な矢印を、また各格子の中央に圧力の計算点を描くべきですが、簡略化して描画しています。）

注1
例外として、Arbitrary Lagrangian Eulerian (ALE)法のように格子を変形させる方法もあります。

2. 粒子法

パイプの中の水の流れ（図１）を粒子法で計算する際の模式図を図３に示します。粒子（計算点）を使って流体を分割します。格子は使いません。ある小さな流体領域を１つの流体粒子で表し、流体の全体を粒子の集合で表すということです。差分法とは異なり、粒子法の計算点は移動します。計算点の移動速度は、その流体粒子の速度となります。図４のような複雑に表面形状が変わっても、この計算点の移動により動画１に示すように簡単に対応できるのです​。

粒子法が簡単なもう１つの理由は、差分法で必要な移流項注2の計算をする必要が無いからです。移流項とは、流体のように位置が時々刻々移動する物体のある物理量（速度、温度など）の時間変化を、空間に固定された計測点での情報のみを用いて求める際に必要となる項のことです。この移流項の計算は複雑になることが多いのですが、粒子法の場合は（計算点を流れとともに移動させるおかげで）移流項を計算する必要がなく、簡単なのです。

具体的な例として、流体の温度の時間変化を求める場合で差分法と粒子法を比較してみましょう。差分法では場所を固定して温度を計測し続けるのに対して、粒子法ではある流体粒子に着目しその粒子の温度を計測し続けるという違いがあります。この観測方法の違いにより、粒子法では移流項を計算する必要がなく簡単なのです。ここでは温度の時間変化の場合で説明しましたが、流速の時間変化でも同様です。差分法では空間に固定した位置で流速の変化を考え、粒子法ではある流体粒子の流速の変化を見ます。

（矢印は流速を表しています。本当は全ての粒子に流速を表す矢印を、また粒子の中心に圧力を表す点を描く​​べきですが、簡略化して描画しています。）

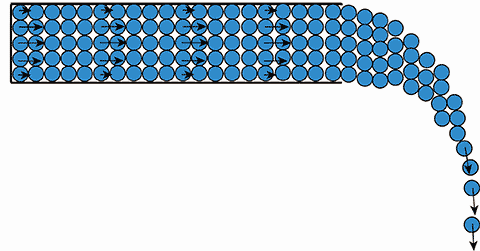
注2
移流項は、ある位置の上を今まさに通過しようとする流体の物理量の時間変化を、空間に固定された位置での情報のみを基に求めようとする際に現れる項です。次の時刻に流体の位置が変わる（下流に流れる）ことに起因する物理量の変化を移流項は表します。もう少し具体的に言うと、流体の微小な塊が現在の場所から下流の場所に移動しようとするときに、同時刻において両者の位置で物理量にあらかじめ差がある場合の影響を表します。

移流項を数式でしっかり理解したい人は、連続体力学や流体力学の教科書[1,2]、粒子法入門[3]を読むことをお勧めします。多くの教科書では、実質微分やラグランジュ微分などの節で移流項を説明しています。ただし、粒子法では移流項は計算する必要がないので、しっかり理解できなくても心配する必要はありません。「粒子法では移流項という面倒な項を計算する必要がなくて簡単だ。」ということを理解いただければ、まずは十分だと思います。