-
陰解法
未来の未知数を求める際に、未来の未知数を含む関係式を解くことで未知数を求める方法。
(関連:半陰解法) -
陽解法
未来の未知数を求める際に、未来の未知数を含めずに現在の既知の値のみを用いて未知数を求める方法。
(関連:半陰解法) -
運動方程式
運動を記述する方程式。流体の場合の運動方程式はナビエ・ストークス方程式で表すことができる。
(関連:ナビエ・ストークス方程式) -
ナビエ・ストークス方程式
流体の運動方程式である。流体に働く力と加速度の関係を表す。
(関連:運動方程式) -
グラディエントモデル
ナブラ演算∇を、コンピュータで計算できる演算(四則演算など)で近似したモデル。勾配モデルとも言う。
(関連:ラプラシアンモデル、四則演算) -
勾配モデル
グラディエントモデルのこと。
(関連:グラディエントモデル) -
ゴースト粒子
計算に関与しない粒子。書籍によっては、ダミー壁粒子をゴースト粒子と呼ぶ場合がある。
(関連:壁粒子) -
影響半径
ある位置での局所的な物理量(密度や、圧力の勾配値、速度のラプラシアンをとった値など)を求める際に用いる半径。この半径内に存在する粒子の数を重みをつけて数えたり、物理量の重み付き平均をとることがよく行われる。
-
オイラー記述(オイラー表示)
空間に固定した点(観測点のようなもの)において、運動を記述する方法。
(関連:ラグランジュ記述) -
重み関数
近傍粒子の影響の大きさを表すための関数。または重み付き平均の計算に用いる関数。粒子法の粒子数密度(重みをつけた粒子の数)、グラディエントモデルや、ラプラシアンモデルなどに使用される。
(関連:粒子数密度、グラディエントモデル、ラプラシアンモデル) -
時間刻み幅
1タイムステップを経過する際に進める時間の間隔のこと。数値計算上、時間は連続的ではなく離散的である。映画のコマ送りのように現在のタイムステップステップkの時刻から次のタイムステップk+1の時刻に時間を変化させる。この2つのタイプステップ間の時刻の差のことを時間刻み幅という。
(関連:クーラン数、拡散数) -
四則演算
足し算、引き算、掛け算、割り算の計4つの基本的な演算のこと。
(関連:グラディエントモデル、ラプラシアンモデル) -
物質時間微分
ラグランジュ微分や実質微分ともいう。ある物理量の時間微分(単位時間当たりに変化する物理量の量)を物体の変形や、流れの移動に追従した位置(観測点)で求める方法。同じ物質粒子を追跡しながら、常に同一の粒子において時間微分をとった値ともいえる。
(関連:ラグランジュ記述) -
質量保存則
質量が保存するという法則。流体の質量保存則は、連続の式で表される。
(関連:連続の式) -
運動量保存
運動量が保存するという法則のこと。流体の運動量保存則は、ナビエ・ストークス方程式で表される。
(関連:ナビエ・ストークス方程式) -
支配方程式
現象を表す方程式のこと。粒子法の支配方程式は、連続の式とナビエ・ストークス方程式である。
-
自由表面
自由に変形することができる境界面のこと。異なる種類の流体の境界部(液体と気体の間など)に存在する。
-
自由表面の粒子
自由表面上(または自由表面に接する)粒子のこと。通常、自由表面上の粒子に何らかの境界条件(圧力を0Paに固定するなどなどの条件)を与えることが多い。
-
重力項
運動方程式において重力による加速度の影響を表す項。
(関連:ナビエ・ストークス方程式、外力項、圧力勾配項、粘性項、対流項) -
初期粒子間距離
粒子法の計算では、計算の初期に粒子をx,y,z方向に等間隔に並べることが多い。この粒子の間隔のこと。
(関連:空間解像度) -
外力項
-
ダミー壁粒子
圧力の変数を持たない壁粒子のこと。粒子数密度などの計算に用いられる。圧力や圧力勾配の計算の際に、ダミー壁粒子は除外される。
-
表面張力
流体の表面に働く張力。
-
CSFモデル
表面張力モデルの1つ。CSFはContinuum surface forceの略。
-
SMAC法
Simplified Marker and Cell法の略。
(関連:タイムマーチング法) -
フリースリップ境界(すべり境界)
壁面において流体と壁面の間で粘性が働かず、流体がすべり流れる境界条件。
(関連:ノースリップ境界) -
ノースリップ境界(すべり無し境界)
壁面において流体と壁面の間で粘性が働き、壁面上において流体の速度がゼロになるような境界条件。
(関連:フリースリップ境界) -
MKS単位系
距離をメートル(m)、質量をキロメートル(km)、時間を秒(s)の単位で表す単位系のこと。
-
圧力勾配項
ナビエ・ストークス方程式やオイラー方程式において、圧力に関する勾配に比例した力の影響を表す項。圧力項とも言う。
(関連:ナビエ・ストークス方程式、粘性項、外力項、対流項) -
ガウスの消去法
-
カーネル関数
Smoothed Particle Hydrodynamics (SPH)という計算手法で使われる関数。MPS法の重み関数に近い使われ方をする。
-
水柱崩壊
柱状に設置した水(初速度は0m/s)が重力で崩れる現象。ダム崩壊とも言い、水を溜めたダムが一度に崩壊して流れ動くような現象である。
(関連:ダム崩壊) -
ダム崩壊
水柱崩壊のこと。
(関連:水柱崩壊) -
スロッシング
タンクなどの容器の中にある液体が地震などで揺らされて液面が激しく揺れ動く現象。
-
規格化
ある関数を積分範囲で積分したときの値が1になるようにする操作。またはあるベクトルに適当な定数をかけてベクトルのノルムを1にする操作。
-
境界条件
圧力計算や粘性計算の際に、壁面や自由表面などの境界部に与える条件。
-
共役勾配法 (Conjugate gradient method)
連立一次方程式を解く解法。反復法の1つ。
(関連:ガウスの消去法) -
距離関数
計算格子の格子点に、その格子から物体や壁面までの距離のデータを持たせたデータの集合のこと。
(関連:ポリゴン壁) -
近傍粒子
ある粒子iの近くに存在する粒子jの集合のこと。
(関連:バケット) -
近傍粒子探索法
近傍粒子を探索する方法のこと。計算領域を分割する方法(領域分割法)などがある。
(関連:バケット) -
空間解像度
シミュレーションを行う際に、空間を離散化する際の大きさのこと。粒子法のシミュレーションでは、粒子サイズを指す。
(関連:初期粒子間距離) -
クーラン数
速度をu、空間解像度をΔx、時間刻みの幅をΔtで表したときに、c=uΔt/Δxで定義される数cをクーラン数という。陽解法では安定に計算できる時間刻み幅の上限が、このクーラン数の大きさで表される場合が多い。
(関連:拡散数、時間刻み幅) -
拡散数
拡散係数(動粘性係数など)をν、空間解像度をΔx、時間刻みみの幅をΔtと表したときに D=νΔt/(Δx)2 で表される数Dを拡散数という。陽解法の場合、拡散現象を安定に計算するには、この拡散数がある一定値以下になるよう時間刻みの幅または空間解像度を設定する必要がある。
(関連:クーラン数、時間刻み幅) -
ソースターム
ポアソン方程式の右辺。
(関連:ポアソン方程式) -
ダイバージェンス
-
タイムマーチング法
時間進行法のこと。
-
格子法
計算格子を使って空間を分割する計算手法のこと。差分法や有限要素法が代表的な格子法である。
-
高粘性流体
粘度が極めて高い流体のこと。
-
コンパイラ
ソースプログラム(プログラミング言語で書かれているプログラム)をコンピュータで実行できる形式のプログラム(機械語のプログラム)に変換するプログラムのこと。Visual Studio、gcc、intel compiler、Xcodeなどが代表的なコンパイラである。
-
拡散方程式
拡散現象を表す方程式。
-
勾配ベクトル
ある物理量の空間的な傾きを表すベクトル量。
(関連:グラディエントモデル) -
対流項
実質微分をオイラー表示した場合に現れる項。流れによって移動することによる加速度の影響を表す項である。
(関連:ナビエ・ストークス方程式、圧力勾配項、粘性項、外力項) -
可視化
計算結果などを視覚的に見えるように描画すること。
(関連:マーチングキューブ法、メタボール) -
フラクショナルステップ法
未知数を求める際に1度に解(未知数)を求めるのではなく、問題を部分的に解く操作を段階的に行うことで解を求めること。部分段解法とも言う。
-
部分段解法
フラクショナルステップ法のこと。
(関連:フラクショナルステップ法) -
壁重み関数
ポリゴン壁(壁粒子を用いずに壁面を表現する方法)で使用する関数。壁粒子が仮想的にあるとしてあらかじめ壁による寄与を求めて関数として表したもの。粒子数密度の計算の際に、壁重み関数を用いる。
(関連:ポリゴン壁) -
壁粒子
壁面を構成する粒子のこと。圧力値を持ち、計算上は基本的には動かない流体粒子として表される。
(関連:境界条件) -
偏微分演算子
偏微分で表される演算子。グラディエントやラプラシアンは偏微分演算子である。
(関連:グラディエントモデル、ラプラシアンモデル) -
ディリクレ境界条件
偏微分方程式を解く際に、境界部の値を直接指定してその値に固定する方法。
(関連:ノイマン境界条件) -
ナブラ
∇記号で表される演算。
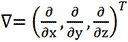 で表され、各方向に関する偏微分の演算を成分にもつベクトル。
で表され、各方向に関する偏微分の演算を成分にもつベクトル。
(関連:ラプラシアン、グラディエントモデル、離散化) -
ポアソン方程式
∇2P=bという形で表される偏微分方程式。ここでbはソースタームと呼ばれ、Pを含まない変数や定数である。
(関連:ソースターム) -
ポテンシャルモデル
-
ポリゴン壁
壁面を壁粒子ではなくポリゴン(Polygon, 多角形)の集合で表す方法。壁粒子を設置する必要がなく、粒子の数を低減することができる。また壁面粒子と比べて滑らかな境界面を表すことができる。
-
マルチフイジックス
複数の物理現象のこと。例えば流体の流れ、構造物の変形、剛体の運動などの現象が2つ以上同時に起こる現象を指す場合が多い。
-
ラグランジュ記述
物体の変形や、流れに追従して常に位置を移動させる観測位置において、物体や流体の運動を記述する方法。粒子法ではラグランジュ記述が使用される。
(関連:オイラー記述) -
ラグランジュ微分
物質時間微分と同じ。
(関連:物質時間微分) -
OpenMP
並列計算のためのライブラリ。共有メモリ型の並列計算を行うことができる。
(関連:MPI) -
ラプラシアン
∇2の演算子。
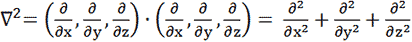 の関係がある。
の関係がある。
(関連:グラディエント、ダイバージェンス) -
ラプラシアンモデル
∇2という偏微分の演算子をコンピュータ上で実行できる演算(四則演算など)に変換するモデル。
(関連:ラプラシアン、グラディエントモデル、離散化) -
四則演算
足し算、引き算、掛け算、割り算の4つの基本的な演算のこと。
-
乱流
不規則な乱れがある流れ。乱れがない層流に比べて流体内で運動量や熱の交換が活発に行われる。
-
連続の式
流体の質量保存を表す式。流体の支配方程式の1つ。
(関連:支配方程式、ナビエ・ストークス方程式) -
離散化
空間や時間をある幅で区切り、区切られたそれぞれの空間や時間における物理量を、ある代表値で表す操作。コンピュータでは連続的な量を表すことは難しく、通常この離散化された値を計算することになる。
-
粒子間相互作用モデル
∇や∇2を近似するためのモデル。近似された式は、近傍粒子と相互作用する形で表されるため粒子相互作用モデルと呼ばれる。
(関連:グラディエントモデル、ラプラシアンモデル) -
粒子数密度
重みを掛けて数えた近傍粒子の数。粒子数密度を用いて流体密度の変化率を表すことにより、圧力が計算される。また自由表面粒子の判定にも用いられる。
(関連:重み関数、自由表面、状態方程式) -
粒子の質量
粒子法において、それぞれの粒子(計算点)が持つ質量。
-
粒子番号
それぞれの粒子(計算点)がもつ識別番号。
-
MPI
並列計算のためのライブラリ。共有メモリ型と分散メモリ型の両方の並列計算が可能である。
(関連:OpenMP) -
濡れ性
-
メタボール
粒子の集合の描画方法の1つ。各粒子に濃度分布を与え、濃度がある一定値となる面を描く方法。
(関連:可視化、マーチングキューブ法) -
音速
音が伝わる速度のこと。
(関連:状態方程式) -
状態方程式
圧力と密度などの関係を表す式。
-
粘性項
運動方程式において、粘性による力の影響を表す項。
(関連:ナビエ・ストークス方程式、圧力勾配項、外力項) -
ノイマン境界条件
偏微分方程式を解く際に、境界部の値を直接固定するのではなく、微分の値を固定する方法。
(関連:ディリクレ境界条件) -
バケット
近傍粒子の探索にかかる計算量を低減するために計算領域を小領域に分割したときの小領域のこと。
(関連:近傍粒子、近傍粒子探索法) -
半陰解法
-
粒子法
連続体を粒子と呼ぶ計算点を用いて離散化し、シミュレーションする手法のこと。このホームページでは粒子法はMoving Particle Semi-implicit法を指す。(補足:Discrete Element Methodなどの非連続体を扱う粒子法もある。)
-
流体摩擦
流体の粘性によって生じる摩擦。
(関連:粘性項) -
流体密度
流体が持つ単位体積当たりの質量のこと。単位はkg/m3で表される。
(関連:粒子数密度) -
v&v
Verification and validationの略。シミュレーションにおいてVerificationは、シミュレーション結果を理論値や他の計算結果と比較することで検証することを表す。Validationは、シミュレーション結果を実験値と比較することで検証することを表す。
-
SOR法 (Successive Over-Relaxation)
連立一次方程式を数値的に解く解法。反復法の1つ。
(関連:共役勾配法) -
マーチングキューブ法
粒子の集合の描画方法の1つ。各粒子に濃度分布を与え、濃度がある一定値である面を三角形の集合で表す方法。メタボールの描画方法の1つ。
