粒子法のいま
粒子法は,偏微分方程式を空間離散化して解く近似解法の一つです.空間離散化方法としては,差分法,有限要素法がよく知られていますが,これらの方法は点だけでなく点の結合情報(メッシュ)を必要とします.たとえば,図1(a) に示す固体に外力を作用させたときの変形を有限要素法で解くと,同図中には(b) に示すように変形に併せてメッシュもゆがみます.粒子法では,図2に示すように,計算したい点と近く(一定の距離以内)に存在する点の情報のみを使って計算が可能であり,計算をする上で仮想的に設けた粒子が物質の移動に併せて自由に動き,また各粒子が自由に動くことができることが最大の特徴です.粒子法は比較的に新しい計算手法で,改良されながら現在も成長・発展を続けている方法です.ここでは粒子法の現状(いま)をお伝えします.
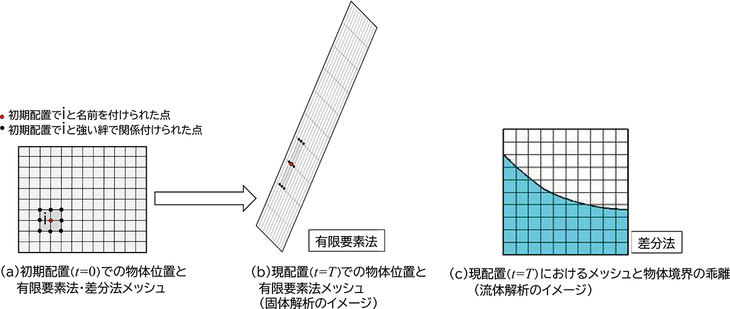
図1 有限要素法・差分法のイメージ図
粒子法の特徴と発展経緯
冒頭の説明の通り,差分法や有限要素法は,点とメッシュを使って計算します.これらのメッシュ型解法では,たとえば流体解析のように,境界が大きく変形・分裂・結合する現象を解くには,図1(c) に示すように計算用のメッシュと実際の物理界面が異なってくるため,界面追跡法や界面補足法などの特別な処理が必要となります.これに対して粒子法は,粒子と呼ばれる点のみから解析が実行できるので,たとえば固体解析においては大変形解析・亀裂進展を含む破壊現象,また流体解析においては自由表面流れ・飛沫等が発生する(分裂・結合を繰り返す)激しい流れに適している数値解法です.また粒子法では,解析領域内部に粒子を配置すれば良いため,メッシュを定義することが困難な複雑な形状を持つ問題では,解析モデルを作成するのが楽になることもメリットになり得ます.一方で,粒子法は開発の歴史が浅いこともあり,未解明な点が残されているのも事実です.特に,解析の誤差評価が不十分であること,また粒子は物体表面に必ずしも設定しなくても良いため(メリットの半面),境界条件の付え方が煩雑になる点がデメリットとなるでしょう.ただし,最近の研究により,解析精度や計算安定性についても随分と改善されつつあります.
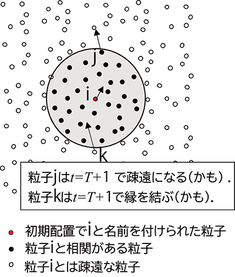
図2 粒子法のイメージ図
この解説では,代表的な粒子法であるSPH(Smoothed Particle Hydrodynamics) 法とMPS(Moving Particle Semi-implicit) 法を具体的に取り上げ,両手法の類似性を説明したのちに,誤差の主要因の一つである粒子分布についての数値実験例について示しながら,最近の粒子法の改良方法等の特徴についてまとめて紹介することにしました.ちなみに,粒状体あるいは複数の剛体ブロックの解析手法として利用される粒子型の数値解析手法としては,個別要素法(DEM:Distinct/Discrete Element Method)があります.これは,各粒子間の相互作用力を経験則あるいは物理の法則によって等価なバネおよびダッシュポットにより近似するものであり,支配方程式となる偏微分方程式の近似解法として位置づけられる粒子法とは概念自体が異なるため,説明の対象外とします.
SPH 法は,1977 年,天体物理(天体の衝突問題など)の解析手法としてLucy[1] とGingoldら[2] によって提案された手法です.その後,1990 年代前半には圧縮性流体の解法[3] へ,1990年代後半には非圧縮性流体の解法[4] へと発展し,またそれと同じくして1990 年以降に例えばLibersky ら[5] により固体の解析手法へと解析対象を拡大されてきました.SPH 法の基本的な考え方は,平滑化関数(smooth function)と呼ばれる重み関数を用い,求めたい関数を“滑らかな関数” で近似することです.この平滑化関数は粒子ごとに定義されます.この近似関数を直接微分することで,勾配やラプラシアンの近似モデルを導出し,これらの近似モデルを用いて微分方程式を近似的に解くことができます.
一方,越塚らによって提案されたMPS 法[6, 7] もSPH 法に似た粒子法として知られていますが,開発の経緯,コンセプトが多少異なっています.まず,MPS 法はSPH 法とは異なり,非圧縮性流体の解析手法からスタートしました.MPS 法は,非圧縮性流体の解析手法の一つである半陰解法(速度は陽的,圧力は陰的に時間積分を行う)の射影法を粒子法に導入した初めての方法であり,のちに初期のSPH 法と同様に圧縮性流体の解法を採用した完全陽解法へと発展しています.また,MPS 法における空間微分の近似は,関数のテイラー展開に基づいた粒子間の相互作用の重み付き平均として導出できます(詳細は次回解説の予定).この空間微分の近似モデルを用いれば,あとはSPH 法と同様に,微分方程式を近似的に解くことができます.
以上の説明の通り,SPH 法では圧縮性流体から非圧縮性流体へ,MPS 法では非圧縮性流体から圧縮性流体へと,流体解析における時間積分方法,非圧縮性の取り扱いなどの発展・開発の経緯が逆転していますが,現在では時間積分方法を含めて大差はありません.両者の主な違いは,空間離散化方法,すなわち空間微分の近似方法にありますが, これについては次回コラムにてご紹介します.
参考文献:
[1] L. B. Lucy: A numerical approach to the testing of the fission hypothesis, Astronom. J., Vol. 82, pp. 1013–1024, 1977.
[2] R. A. Gingold and J. J. Monaghan: Smoothed particle hydrodynamics: Theory and application to non-spherical stars, Monthly Not. Roy. Astronom. Soc., Vol. 181(3), pp. 375–389, 1977.
[3] J. J. Monaghan: Simulating free surface flows with SPH, J. Comput. Phys., Vol. 110, pp. 399–406, 1994.
[4] S. J. Cummins and M. Rudman: An SPH projection method, J. Comput. Phys., Vol. 152, pp. 584–607, 1999.
[5] L. D. Libersky and A. Petschek: Smooth particle hydrodynamics with strength of materials, in Advances in the free-Lagrange method including contributions on adaptive gridding and the smooth particle hydrodynamics method, Springer, pp. 248–257, 1991.
[6] S. Koshizuka and Y. Oka: Moving-particle semi-implicit method for fragmentation of incompressible fluid, Nuclear Sci. Eng., Vol. 123, pp. 421-434, 1996.
[7] 越塚誠一:計算力学レクチャーシリーズ5 粒子法, 日本計算工学会編, 丸善, 2005.


