粒子法の1つであるMPS(Moving Particle Semi-implicit)法では、非圧縮性流体を「密度一定」であるとして解いています。一方、有限体積法などの格子法では「速度の発散ゼロ」を使います。この違いがMPS法の特徴の1つなので、その違いについてここでは解説します。
粒子法の研究を開始した1993年に、既にSPH(Smoothed Particle Hydrodynamics)という粒子法がありましたが、陽的なアルゴリズムを用いて圧縮性流体を解く方法でした。工学的な流体力学の問題の多くは非圧縮性流体であり、格子法では半陰的なアルゴリズムを用いて解かれていました。そこで、半陰的アルゴリズムを用いて非圧縮性流体が解けるような粒子法を模索していました。そうしてたどり着いたのがMPS法です。ただ、これまでの格子法とは少し変えていまして、そこがMPS法の特徴であり、肝心かなめの中心部分になっています。
そもそもから話を始めると、物理の基本的な保存則は3個あり、質量保存則、運動量保存則、エネルギー保存則です。エネルギー保存則は質量保存則と運動量保存則から導くことができるので、実際には2個を解けば答えが出ます。流体力学では、質量保存則は「連続の式」、運動量保存則は「ナビエ・ストークス方程式」と呼ばれており、これら2個の式を解いています。粒子法でもそうです。非圧縮性が関係するのは質量保存則すなわち「連続の式」です。
圧縮性流体の連続の式は
$$ \frac{D \rho}{D t}+\rho \nabla \cdot \boldsymbol{u}=0 $$です。非圧縮性流体では、式(1)の左辺の第1項がゼロであり、従って第2項もゼロになります。
$$ \frac{D \rho}{D t}=0 $$ $$ \nabla \cdot \boldsymbol{u}=0 $$さらに、式(2)を時間で積分した式、すなわち密度\(\rho\)が時間的に一定であるという式
$$ \rho=\it{const} $$も得られます(式(4)の右辺の\(\it{const}\)は一定値の意味)。
式(4)は「密度一定」ということなので、各時刻で密度を計算して、それらを一定値にしなさいということを意味します。これをMPS法では課しています(Koshizuka and Oka, 1996)。一方、格子法では式(3)すなわち「速度の発散ゼロ」を使います。粒子法でも「速度の発散ゼロ」を使うこともできます。いったいどの式が非圧縮条件として本質的なのでしょうか。あるいは、どれを課しても同じと考えていいのでしょうか(図1)。
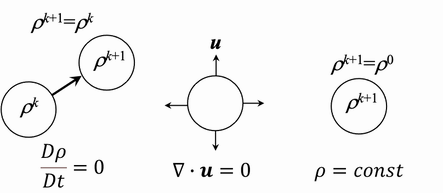
図1 非圧縮条件はどれが本質的なのか?
まず、式(4)と式(3)は何が違うのかを考えてみましょう。そもそもに話を戻すと、連続の式は質量保存則です。これは、質量が一定であるという意味であり、非圧縮性流体では本質的には式(4)です。式(4)を時間で微分すると、密度の時間変化はゼロであるという式(2)が得られ、式(1)を介して「速度の発散ゼロ」という式(3)が得られます。
貯金にたとえると、毎月、貯金の総額が一定であることを残高から確認するのが式(4)で、出金と入金の総計がゼロであることを確認するのが式(3)です。計算を間違えなければ、どちらも同じことですが、もし、計算に間違う可能性がある場合には、残高を確認する前者の方が直接的すなわち本質的ではないでしょうか。
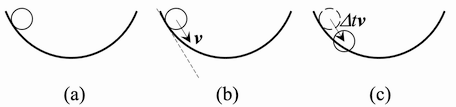
図2 斜面上に拘束される玉の運動
また、図2(a)のような斜面上を転がる玉を考えます。玉は斜面上に存在しなければならないというのが直接的な拘束条件であって、流体力学における式(4)に対応します。玉が斜面上に存在しなければならないという条件を時間で微分すると、玉の速度\(\boldsymbol{v}\)が斜面と平行でなければならないという条件が得られます(図2(b))。こちらは式(3)に対応します。この時、次の時刻の玉の位置への移動を、\(\boldsymbol{v} \times \Delta t\)、とすると、図2(c)のように玉は地面に少しめり込むことも考えられます。つまり、瞬間的には、拘束条件=拘束条件の時間微分、なのですが、数値計算では誤差が入り込むので、拘束条件≠拘束条件の時間微分、となってしまいます。そう考えると、図2(a)の方が図2(b)よりも満たすべき拘束条件として本質的です。粒子法でも同様で、式(3)で非圧縮条件を課すと、数値計算の誤差によって流体の密度がわずかずつ変化してしまいます。そして時間とともに変化は蓄積されます。従って、非圧縮条件は式(4)が本質的で式(3)は派生的です。
MPS法より前に開発された粒子法であるSPHにおいても「密度一定」を非圧縮条件として課す方法があります(Shao and Lo, 2003)。この方法はISPH(Incompressible SPH)と呼ばれ、MPS法の非圧縮条件をSPHに取り入れたもので、元の論文(Shao and Lo, 2003)にはそのことが書かれています。
では、粒子法において「密度一定」と「速度の発散ゼロ」のどちらが優れているでしょうか。筆者は、「密度一定」の方が粒子法の特徴であるロバスト性(頑強さ)の点から優れていると考えています。詳細に見れば、それぞれ利点と欠点があります。「密度一定」の利点は、(1) 密度の誤差が蓄積しない、(2) 粒子配置が均等になる、(3) 自由表面境界条件が簡単、というものです。その一方で、圧力が振動しやすいという欠点があります。「速度の発散ゼロ」では利点と欠点は反対になります。そこで、非圧縮条件として式(2), (3), (4)を混ぜるという方法が考案されました(近藤, 越塚, 2008; Tanaka and Masunaga, 2010)。こうした方法ですと、「密度一定」の利点を残しつつ、欠点である圧力振動が改善されます。
参考文献:
S. Koshizuka and Y. Oka, “Moving-Particle Semi-implicit Method for Fragmentation of Incompressible Fluid,” Nucl. Sci. Eng. 123, 421-434 (1996).
S. Shao and E. Y. M. Lo, “Incompressible SPH Method for Simulating Newtonian and non-Newtonian Flows with a Free Surface,” Adv. Water Resources 26, 787-800 (2003).
近藤雅裕, 越塚誠一, “MPS法における不自然な数値振動の抑制,” 日本計算工学会論文集, Paper No.20080015 (2008).
M. Tanaka and T. Masunaga, “Stabilization and Smoothing of Pressure in MPS Method by Quasi-Compressibility,” J. Comput. Phys. 229, 4279-4290 (2010).


